1. Continuous-time Signals
- 푸리에 변환과 그 역변환


신호 x(t)의 푸리에 변환, X(F)의 역푸리에 변환을 통해 원래의 시간 도메인 신호를 복원하는 과정이다.
푸리에 급수는 주기적인 신호를 주파수 성분으로 분해하기 위해 사용되며, 푸리에 변환은 비주기적 신호를 주기적 신호의 주기가 무한대임을 가정하여 주파수 영역으로 변환할 수 있다.
여기서 중요한 조건은 x(t)가 절대 적분 가능(absolutely integrable)해야 한다는 점이다. 주파수 영역에서 다시 말하면 에너지가 유한해야 한다는 것, 시간 영역에서 주기적이지 않거나 시간적으로 제한된 신호여야 한다는 뜻이다.
- 푸리에 변환과 에너지 조건

이 조건의 물리적인 의미는 에너지가 유한해야한다는 것이다. 신호 x(t)가 물리적인 세계에서 존재 혹은 유효하기 위해서는 무한한 에너지를 가지면 안 된다.
만약 이 적분이 무한이라면 신호는 에너지가 무한대인 비물리적인 신호가 된다. 물리적으로 에너지가 유한하지 않은 신호는 현실에서 존재하지 않으며 신호 처리 및 변환이 의미를 가지기 위해서는 에너지가 유한해야 한다.
주기 신호는 무한한 시간을 가지므로 절대 적분 가능 조건을 만족하지 않는다. 대신 주기 신호에 대해서는 Fourier series를 사용하여 주기적인 신호를 주파수 성분으로 분해한다. 이로서 주기 신호는 주파수 도메인에서 무한한 값이 아닌 한정적인 이산적인 스펙트럼을 가지게 된다.
* 신호가 주기적, 무한한 신호, 주파수가 무한한 값이라면 푸리에 변환이 안 된다는 뜻? *
그런 뜻은 아니다. 푸리에 변환이 안 된다는 뜻이 아닌 주기 신호에 푸리에 변환을 적용하면 이산적인 주파수 성분들로만 표현된다. 이는 Dirac delta function을 사용하여 설명할 수 있다.
다시 말하면 주기적인 신호를 분석하는 것은 의미는 있지만 현실에서 무한한 주기신호는 존재하지 않다는 뜻이다. 말 그대로 물리적으로는 신호가 존재하지 않는다. 주파수 영역에서 신호 처리 및 변환을 할 수 없다는 뜻이다.
* 간단 용어 정리 *
- 각주파수 (ω, angular frequency [rad/s])
신호의 주기를 나타내는 주파수의 라디안 단위 표현이다. (ω=2πf)
주기적인 신호에서 각 주파수는 시간에 따라 신호가 얼마나 빠르게 진동하는지를 나타낸다. 주파수를 라디안 값으로 나타낸 것이라 볼 수 있다.
- 주파수 (f, frequency, [Hz])
신호가 1초에 반복되는 획수로 주기의 역수이다. (f=1/T)
주파수는 1초 동안 신호가 몇 번 반복되는지를 나타내며 신호의 반복성을 정의하는 개념이다.
- 위상 (phase, φ, [rad, 도(°)])
주파수 성분의 시간적 변이를 나타내는 값이다. 신호의 특정 주파수 성분이 기준 시간에 비해 얼마나 앞서거나 뒤서 있는지를 나타낸다.
2. 푸리에 변환의 주요 특성
- 선형성 (Linearity)


주파수 영역에서 선형 결합은 그대로 선형성을 유지한다.
- 시간 이동(Time shift)


주파수 영역에서 지수 함수 곱은 위상 변화를 나타내며 크기는 변화지 않는다.
- 시간 및 주파수 스케일링(Time and frequency scale)
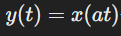

스케일링은 주파수의 변화와 크기도 영향을 준다. 시간 영열에서 신호가 압축되거나 확장되면 주파수 영역에서도 변화가 발생한다.
- 시간 영역에서의 컨볼루션(Time-domain convolution)


시간 영역에서의 컨볼루션은 주파수 영역에서의 곱셈으로 대응된다. 필터링 동작과 관련하여 LPF(Low-Pass-Filter)는 주파수 영역에서 신호의 곱 형태로 표현된다.
3. 푸리에 변환을 통해 얻을 수 있는 유용한 성질을 알아보자.
- Parseval 정리
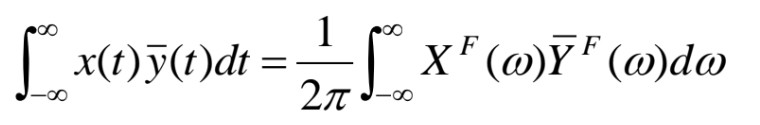
시간 신호와 그의 푸리에 변환된 주파수 신호 간에 직접적인 물리적 유사성이 없지만 두 영역에서 신호의 전체 에너지가 동일하게 표현된다는 것이다. 즉, 신호의 전체 에너지가 시간 도메인에서의 적분과 주파수 도메인에서의 적분이 같다는 것이다.
* 에너지가 같다는 의미 *
- 시간 도메인에서의 에너지
신호 x(t)가 있을 때 그 신호가 얼마나 강한지를 나타내는 값이다. 시간에 따라 신호의 제곱을 적분하면 전체 에너지를 구할 수 있다. 즉, 신호가 얼마나 오랫동안, 얼마나 큰 값을 가지는지 측정한다.
- 주파수 도메인에서의 에너지
같은 신호를 푸리에 변환하면 주파수 성분 X(f)가 생성된다. 이 주파수 성분의 제곱을 적분해도 전체 에너지를 구할 수 있다. 이는 신호가 어떤 주파수에서 얼마나 강한지를 나타낸다.

* 적분의 순서를 재배치할 수 있는 이유 *
푸비니의 정리에 의해서 가능하다. 적분이 수렴할 때 곱을 각각의 변수에 대해 독립적으로 적분할 수 있다는 것이다.

이 적분을 먼저 x에 대해 적분을 한 뒤 그 결과에 대해 y 적분을 수행할 수 있다. 이는 적분의 순서를 바꿔도 동일한 결과를 얻을 수 있다.

x 적분, y 적분에 대해서 순서대로 적분할 수 있다는 것은 각각 적분해도 된다는 것으로 해석할 수 있다.

증명식에서는 이를 역순으로 나눠져있는 적분을 하나로 합친 것이다.
- 대칭성

4. 주기적인 연속 신호는 푸리에 시리즈의 역변환으로 표현한다.

주기적인 연속 신호는 푸리에 시리즈를 사용하여 표현할 수 있으며 이 시리즈는 신호를 주파수 성분의 합으로 분해하는 방법이다. 주기 T를 갖는 연속 신호이다.

푸리에 시리즈는 모든 정수 k에 대해 각 성분을 더하는 형태이다.
5. DT(Discrete Time, 이산 시간) 신호를 푸리에 변환을 통해 해석!
- 신호 정의
- 이산 신호 x[n]: 연속 시간 신호를 샘플링하여 얻은 신호로 x[n] = x(nT)로 정의된다. n은 정수이고 T는 샘플링 주기이다.
- 푸리에 변환
- 이산 신호의 푸리에 변환 X(θ): 이산 신호 x[n]의 주파수 도메인 표현이다.

- 역푸리에 변환: 주파수 도메인에서 정보를 시간 도메인으로 복원하는 과정이다.
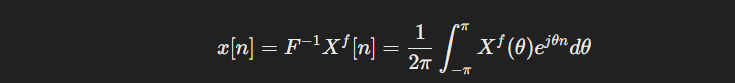
- 주요 성질
- Linerity(선형성)

- Time shift(시간 이동)

- Time-domain convolution(시간 영역의 컨볼루션)

6. 푸리에 변환의 주기성 특성
이산 신호 x[n]는 샘플링을 통해 얻어진 연속 시간 신호의 샘플이기 때문에 주기적으로 반복되는 특성을 가진다. 이 때, 이산 신호의 푸리에 변환도 이러한 주기성을 반영한다.
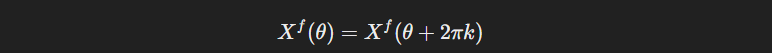
이는 주파수 도메인에서 신호가 2π 주기로 반복됨을 나타낸다. 이로 인해 주파수 성분들이 주기적으로 배열되는 이산 신호의 특성을 가진다.
* 왜 연속 푸리에 변환은 주기적이 않지만 이산 푸리에 변환에서는 주기적일까? *
- 이산 신호와 연속 신호의 본질적인 차이
이산 신호는 시간축에서 특정 샘플링 간격으로 신호를 끊어서 표현한 것이다. 샘플링이 발생하면서 주기적으로 반복되는 성질이 생긴다.
연속 신호는 시간축이 연속적이므로 샘플링 없이 모든 시간에서 신호가 존재한다. 따라서 신호 자체가 주기성을 가져 여러 주파수 성분을 가지지 않는 한 푸리에 변환 결과도 주기적이지 않다.
- 지수 함수와 주기성, 연속 푸리에 변환에서의 차이
이산 신호의 푸리에 변환에서 사용하는 지수 함수는 에 대해 주기성을 가진다.

이산 신호의 경우 n은 항상 정수이기 때문에 θ+2π가 θ와 동일한 값으로 취급된다. 이로서 이산 푸리에 변환은 주기적인 특성을 가진다.
연속 푸리에 변환에서 사용하는 지수 함수에서 t는 연속적인 값을 가진다. 그로 인해 ω+2π는 ω와 같은 값을 가질 수 없다. 즉, ω+2π는 ω와 동일하지 않은 주파수 성분으로 취급된다.
_ 예시

'학부 수업 내용 정리 > 디지털신호처리' 카테고리의 다른 글
| # 10 Fast Fourier Transform (1) (0) | 2024.10.20 |
|---|---|
| #6 Sampling and Reconstruction(3) (0) | 2024.09.23 |
| #4 Sampling and Reconstruction(1) (0) | 2024.09.23 |
| #0 그쪽도 푸리에 변환을 아는지? (0) | 2024.09.04 |
| #1 Introduction to Digital Signal Processing (0) | 2024.09.02 |