주파수 응답 중 magnitude response를 알아보았으니 이제 phase response가 어떻게 되는지를 알아보자.
1. Magnitude Response
1.1. 응답형태
Magnitude response는 두 가지 주요 형태로 나눌 수 있다
- Monotone Response(단조 응답): 크기 응답이 계속 증가하거나 감소하는 형태로 passband에서 stopband로 전환할 때 사용된다.
- Oscillating or Rippling Response(진동 또는 리플 응답): 크기 응답이 진동하거나 리플을 포함하는 형태고 passband와 stopband에서 주기적인 ripple이 나타난다.
1.2. Analog Filter와 Digital Filter의 차이
- Analog Filter: 라플라스 변환을 기반으로 하여 s-domain에서의 유리 함수 형태로 표현된다. 아날로그 필터는 연속 신호를 다루므로 주파수 제한이 없다.
- Digital Filter: z-변환을 기반으로 하며 z-domain 유리 함수 형태로 표현된다. 샘플링된 이산 신호를 다루므로 샘플링 주파수(f_s)의 절반인 Nyquist 주파수 이상에서는 정보가 중복된다. 또한 디지털 신호의 주파수는 주기적이므로 θ의 범위는 제한된다. ( 0≤ θ ≤π )
2. Phase Response
2.1. Trans function을 통해 알아보는 Magnitude response와 Phase response
RCSR (Realizable, Causal, Stable, and Rational) 조건을 만족하는 필터의 주파수 응답으로부터 Magnitude Response와 Phase Response를 구하는 과정을 살펴보자.

Trans function에 절대값을 취해 phase를 제외한 값이 magnitude이고, phase는 magnitude가 음수인 경우도 고려하게 된다.
필터의 크기 (Magnitude)와 응답 (Phase Response)을 구하는 작업은 필터를 설계할 때가 아니라 시스템의 성질을 파악할 때 주로 수행한다.
2.2. Phase response의 두 가지 특징
2.2.1. 불연속 점을 가지는 두 개의 조건
- Trans function의 Magnitude가 0인 경우 Phase에서 불연속이다. 정의가 되지 않기 때문이다.
- Phase가 π, -π를 넘어가는 경우 Phase에서 불연속이다.


2.2.2. 유한 개의 zero

Filter가 RCSR이라면 Filter가 zero가 되는 점의 개수는 유한하다는 의미이며, 이는 phase가 불연속적인 점이 유한하다는 것이다.
또한 z-transform 기반이기 때문에 θ는 -π부터 π까지 제한된다. 이산 신호는 주파수 영역에서 주기적이기 때문이다.
3. Continuous-Phase Representation: 연속 위상을 표현해보자!
지금까지 Trans function이 주어졌을 때 magnitude와 phase의 response를 구하는 방법을 알아보았으며, magnitude가 0인 곳, phase의 값이 -π 혹은 π를 넘어가는 경우 jump가 발생하여 불연속적이라는 것을 파악했다.
이를 바탕으로 예제를 살펴보자.
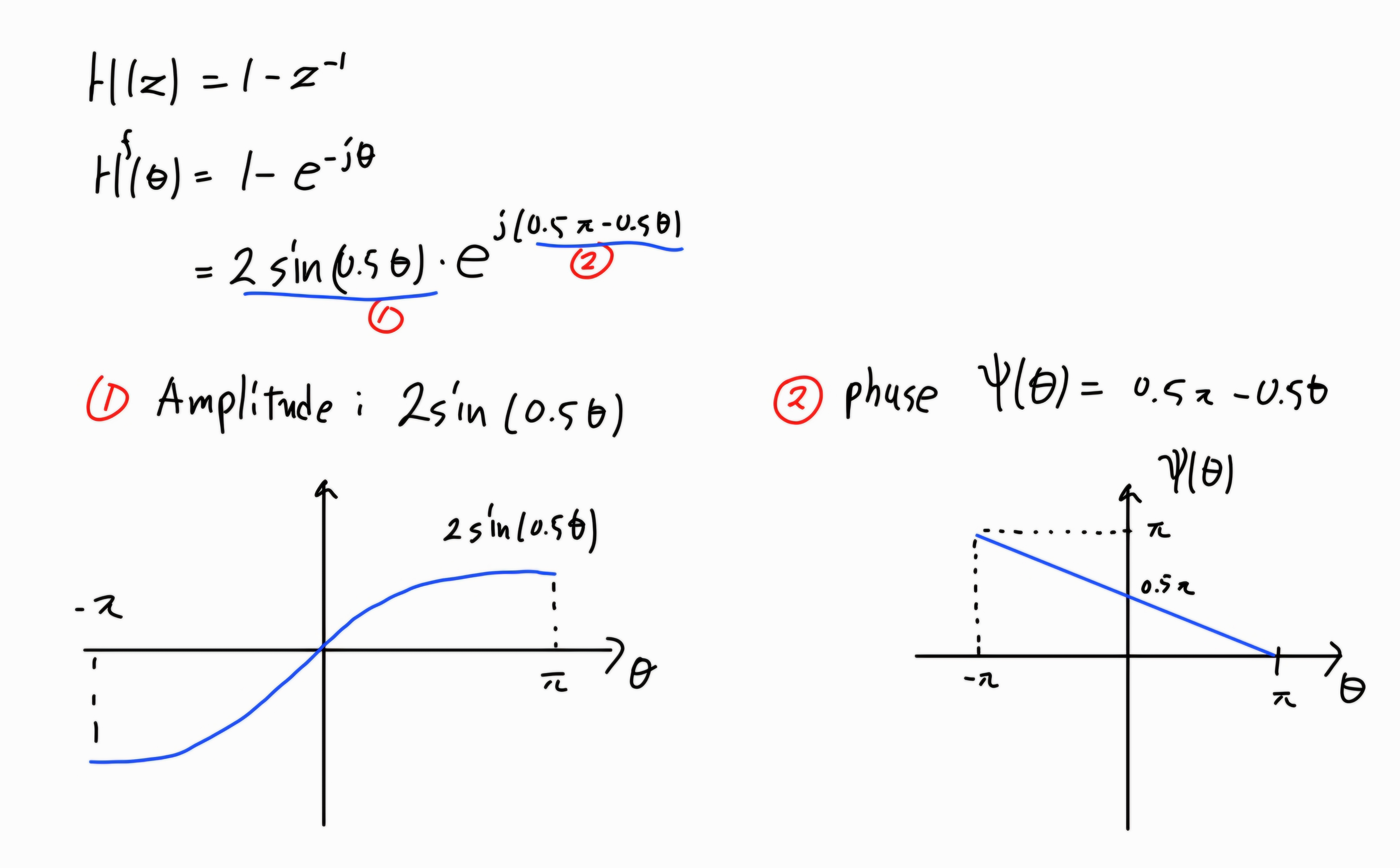
3.1. H(z) = 1-z^(-1)

- frequency를 얻기 위해서는 크기가 1인 복소지수함수와의 곱으로 표현되어야 한다.
이 때, 멀쩡한 값을 대칭으로 위해 반으로 가르는 기법이 필터를 설계할 때 자주 사용된다. - magnitude가 0인 θ에서는 phase가 정의되지 않는다.
- magnitude의 크기는 항상 양수이기 때문에 음수인 부분은 phase가 반전되어 이 때 jump가 발생한다.
기존에 알던 특징과 달리 3번은 새로운 특징으로 나온다. 이를 살펴보자.
3.2. Zero의 차수와 Phase의 연속성
Zero의 차수 m에 따라 phase의 연속성이 달라진다.

Zero의 차수가 짝수라면 magnitude의 부호가 0의 주변에서 부호가 바뀌지 않으므로 phase에서 반전이 일어나지 않는다. Zero의 차수가 홀수라면 magnitude의 부호가 0의 주변에서 부호가 바뀌므로 phase에서는 반전이 일어난다. 즉 jump가 발생한다.
3.3. Amplitude: Magnitude와는 달리 절대값을 취하지 않은 버전
Amplitude는 Magnitude에 절대값을 제거한 버전으로 음수 크기도 포함한다. 이를 통해 위상의 jump 현상을 제거하여 phase의 continuous를 보장할 수 있다.
3.4. Phase가 Discontinuous한 지점
지금까지 배운 내용들을 정리해보자.
- Frequency Response(이자 Filter, Trans function)에서 Magnitude response와 phase reponse를 구하고 싶다.
: 크기가 1인 복소지수함수의 복소수와 곱의 형태로 만든다. 곱하는 항은 magnitude가 된다. - phase가 불연속인 지점
- magnitude가 0: phase는 정의되지 않는다.
- phase의 값이 π, -π를 넘어감: phase는 jump한다.
- magnitude의 부호가 바뀐다(zero의 차수가 홀수, 짝수면 phase는 연속): phase는 반전된다. - Amplitude는 phase에서 amplitude의 부호가 바뀌더라도 반전되지 않는다.
4. 이제 linear phase(Delay filter)와 generalized linear phase에 대해 할 건데 인공지능도 급하고 실험도 급해서 걔 먼저 끝내고 오자.
일단 약술하자면 linear phase는 delay로 입력을 지연시킨다
만약 fraction이 있다면 interpolation한다. 보간 사이간 보안한다. = > 마치 sinc 형태
general한 버전도 있다 이는 위상이 더해지는 형태가 아닌 곱해지는 형태라서 다르다 얘는 아직 모르겠다.
이해했다.
딜레이 필터의 특징
딜레이 필터는 시간 지연을 적용하는 필터로, 신호의 과거 값들을 결합하여 평균을 내는 방식으로 동작한다. 이러한 동작은 저역통과(Low-Pass, LP) 필터의 특성과 유사합니다.
FIR 필터와 딜레이 필터
- FIR 필터는 Finite Impulse Response의 약자로, 피드백이 없는 필터입니다. 즉, FIR 필터는 입력 신호를 일정한 수의 지연된 값들에 대한 선형 결합으로 출력 신호를 계산합니다.
- FIR 필터의 주요 특징은 지연 필터들을 결합하여 주파수 성분을 선택적으로 통과시키는 능력을 가진다는 점입니다.
예시로 고주파 성분이라면 신호를 딜레이 즉 과거 값들을 결합하여 평균을 내면 저주파가 나오는 방식을 진행한다.
딜레이 필터와 필터의 계수 분포
딜레이 필터의 계수 분포에 따라 필터의 특성이 결정됩니다. 계수는 **FIR 필터의 계수(weight)**를 말하는데, 이 계수들이 어떻게 분포하는지에 따라 필터가 저역통과(LP), 고역통과(HP) 또는 대역통과(BP) 등의 특성을 가질 수 있다.
또
딜레이 필터의 특징은 딜레이 되는 정도에 따라 이전 값들의 평균으로 나타낼 수 있다. 딜레이 필터는 대표적인 FIR 필터이다. 딜레이 필터는 변화가 큰 고주파를 delay된 만큼 평균을 내므로 고주파 성분은 통과 못하고 저주파 성분만 통과된다.
이런 딜레이 필터는 몇 만큼 딜레이하는 order의 개수와 필터의 계수의 분포에 따라 필터의 종류가 나뉜다. 어떤 계수의 분포는 HP로는 못 쓰인다는 특징이 있다.
FIR 필터는 여러 개의 딜레이 필터가 결합된 구조이다.
delay filter가 어떻게 고주파 저주파를 통과하거나 막을까? 바로 특정 세타 값에 대해 즉, 고주파, 저주파에 대해 delay를 하면 고주파에서 딜레이 즉, 이전 값들을 모두 더해버린다면 그만큼 신호의 고주파는 줄어들고, 저주파 성분, 즉 평균을 곱하게 되므로 값이 특색이 없어진다.
delay를 시키는 모양에 따라 정형화됨
딜레이 필터들의 order와 계수가 대칭인 모양에 따라 filter의 모양이 정형화 되어있다.
FIR 필터가 딜레이 필터인 이유는 모양이 딜레이임. 딜레이여서 뭐할 거냐? 신호 억제
- 딜레이 신호는 평균내버리고 고주파 없애버리는 필터이다
- 내가 보낸 신호에 대해 고주파에서 딜레이 시켜버리면 평균 내버리고 끝이다.
반대로 고주파에서는 통과하고 저주파에서 신호를 평균 크게 내버리면 저주파가 통과 못한다.
- 이러한 필터의 계수들의 개수와 계수의 대칭적인 분포에 따라 필터의 종류가 정형화된다.
phase response를 보며 얻은 특징
- tg는 group delay로 신호가 delay된 정도이다.
- initial phase는 신호가 어디서 시작할지 알려주는 것
- tap: 필터의 계수의 개수
- order: 신호의 지연을 나타내는 항의 최대 차수
- 그룹 지연 τg : = (N−1)/2 (N은 탭의 개수(필터 계수의 길이))
- group delay는 주파수 응답에서 변화율이 정수냐 비정수냐에 따라 integer delay인지 interpolated delay인지 따진다. 실제로는 y[n]=x[n]+x[n−3]와 같은 경우는 현재 샘플과 3샘플 이전을 더하는 시스템에서는 정수 delay가 이뤄지지만 필터의 주파수 응답에서 phase response를 미분한 group delay 입장에서는 fractional delay라고 볼 수 있다.
필터 계수에 따른 필터의 특징 결정: 계수가 홀수면 integer group delay, 짝수면 fractional group delay, initial phase =0이면 대칭, initali phase가 pi/2 반대칭
필터는 real 신호를 다루기 때문에 conjugate symmetry를 만족하게 된다. 이로 인해 나온느 조건으로 Amplitude의 대칭과 반대칭이 있다. 필터의 계수가 대칭이냐 반대칭이냐에 따라 필터의 특징이 있다.
또한 filter의 phase reponse를 봤을 때 phase가 integer phase냐 noninteger phase냐에 따라서 integer group delay, fractional group delay로 나뉜다.
integer group delay와 fractional group delay의 차이는 h[n]의 계수들을 모두 x[n]과 컨볼루션한 값인 y[n]에 대해서
y[n]=x[n-L]
or
y[n]=m을 -무한대부터 양의 무한대까지 더한 경우의 x[m]sinc(n-m-L-delta)
로 표현할 수 있다는 것이다.
즉, H(z)의 계수를 보고 시스템이 어떤 시스템인지를 알 수 있다.
'학부 수업 내용 정리 > 디지털신호처리' 카테고리의 다른 글
| #18 Introduction to Digital Filters(1) - Filter Specification (0) | 2024.11.21 |
|---|---|
| # 15 Review of Z-transform and Difference Equations (1) - Z 변환의 필요성 (0) | 2024.11.06 |
| # 11 Fast Fourier Transform (2) (0) | 2024.10.20 |
| # 10 Fast Fourier Transform (1) (0) | 2024.10.20 |
| #6 Sampling and Reconstruction(3) (0) | 2024.09.23 |