1. Optimization
1.1. 목적 함수 (Objective Function)를 최대화 하거나 최소화한다?
- 최적화의 핵심은 주어진 데이터셋을 바탕으로 특정 목표를 달성하기 위한 함수를 최대화하거나 최소화하는 것이다.
- 예측 값과 실제 값 간의 오차를 최소화하는 것이 일반적인 목표가 된다.
- 예를 들어, 선형 회귀에서는 손실 함수로 평균 제곱 오차(MSE, Mean Squared Error)를 사용하여 목적 함수를 설정한다.
- 주어진 데이터는 이 목적 함수에 따라 평가되며, 모델의 성능을 최적화하는 데 기여한다.
1.2. 인공지능에서의 Optimization
- 최적화는 주어진 문제의 목적 함수를 최대화하거나 최소화하는 과정을 말한다.
- 특정 목적 함수가 설정되어 있으면, 해당 함수에 따라 모델의 파라미터를 최적화하는 방법이 다양하다.
- 예를 들어, 경사 하강법(Gradient Descent)과 정규 방정식(Normal Equation) 같은 기법이 있으며, 이러한 방법들은 데이터에 대한 평가에 따라 파라미터를 업데이트하는 방식을 제공한다.
linear regression이 아니더라도 목적 함수가 MSE인 모델 중 최적화하는 여러 방법에 대해 알아보자.
2. 다양한 최적화 기법
2.1. Newton's Method

- 개요: 비선형 함수의 최적화에서loss funcion의 최소값을 찾기위해 접선을 이용해 다음 x를 구하는 방법이다.
- 장점: 빠른 수렴 속도, 정확한 업데이트
- 단점: 초기값(initial points)에 민감하고, Hesian Matix를 계산하는 비용이 높다.
2.2. Gauss-Newton's Method
2.2.1. 목적
-
실제값과 예측값 간의 MSE을 최소화하는 비선형 최소 제곱 문제를 해결하는 데 사용된다. Objective function이 MSE라는 뜻이며 이를 최소화하는 것이 목적이다.
- linear regression과 달리 비선형적인 모델 또한 측정할 수 있다.
2.2.2. 구현 방법
- Gauss-Newton 방법은 최소 제곱 문제를 풀기 위해 잔차를 MSE하려고 한다.
- 하지만 이때 MSE에 대한 직접적인 미분은 계산이 복잡하다.
- 이를 간소화하기 위해 MSE의 2차항 대신 잔차 자체에 대해 자코비안 행렬을 계산하여 문제를 풀어 나간다.

- 예시: Gauss-Newton's Method를 통한 linear regression 파라미터 추정

F와 J의 부호가 바뀌어도 상관없다. F를 실제값에서 예측값을 빼든, 예측값에서 실제값을 빼든 상관없다.
2.2.3. Taylor series로 유도하는 Gauss-Newton method

2.3. Levenberg method
- Levenberg 방법은 비선형 최소 제곱 문제를 해결하는 알고리즘으로, damping parameter를 사용하여 안정성을 높이는 방식이다.
- damping parameter(λ)의 크기에 따라 알고리즘의 스텝 크기가 조절된다.
- 스텝이 크면: 경사 하강법처럼 loss function의 기울기가 큰 방향으로 크게 업데이트하며 최적화 과정이 빠르게 진행된다.
- 스텝이 작으면: 가우스-뉴턴 방식으로 작동하여 수렴할 지점에 가까워졌을 때 안정적으로 parameter를 업데이트한다.
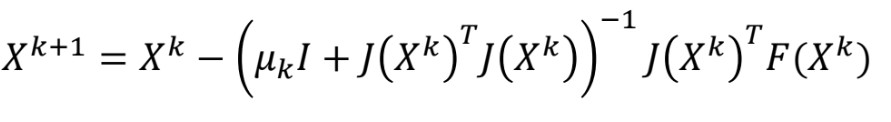
2.4. Levenberg-Marquardt Method
Levenberg-Marquardt 방법은 Levenberg 방법의 확장으로, 각 자코비안 행렬의 대각 행렬을 사용하여 안정성을 더욱 강화한 알고리즘이다.
- Damping Parameter ():
- 단순한 단위 행렬 대신 각 자코비안 행렬의 대각 행렬을 사용하여, 각 파라미터에 대한 damping 효과를 조절한다.
- 이를 통해 각 파라미터의 영향을 균형 있게 조절하여 최적화를 더욱 효과적으로 수행할 수 있다.

'학부 수업 내용 정리 > 인공지능심화' 카테고리의 다른 글
| #10 Linear Classifier (1) (0) | 2024.10.18 |
|---|---|
| #8 Decision Tree (1) (0) | 2024.10.01 |
| #4 Regression(3) (0) | 2024.10.01 |
| #3 Regression(2) (0) | 2024.10.01 |
| #2 Regression에 대하여(1) (0) | 2024.09.22 |