0. AI에게 학습이란?
0.1. AI 학습에 대하여
AI에게 학습이란 input과 output 사이의 관계인 가중치(weight)를 파악하는 과정이라고 배웠다. AI 모델은 주어진 데이터셋을 학습하면서 입력과 출력 간의 패턴이나 규칙을 찾기 위해 weight를 조정한다.
AI로 해결할 수 있는 문제 유형 중 하나인 Regression을 알아보며 학습에 대해 공부해보자.
* ImageNET에 대해 간단히 알아보자 *
ImageNet은 대규모 이미지 데이터셋으로, 약 1400만 개의 이미지에 레이블이 달려 있어 컴퓨터 비전 분야에서 딥러닝 모델을 훈련하는 데 사용된다. 다양한 사물 인식을 위한 표준 자료로, 2012년 ImageNet 대회에서 딥러닝 모델인 AlexNet이 우수한 성과를 내면서 딥러닝의 발전을 크게 이끌었다.
1. Linear Regression의 목표를 이루는 구현체 Hyopthesis Function!
1.1. Regression이란? 그리고 회귀라는 뜻은 무엇을 의미할까?
Regression은 연속적인 값을 예측하는 문제를 다룹니다. 예를 들어, 주식 가격, 집 값, 온도, 또는 특정 시점에서의 수요를 예측하는 것이 대표적인 Regression 문제입니다.
Regression은 Classification 문제(이산적인 카테고리 예측)와는 다르게, 예측 대상이 연속적인 숫자일 때 사용됩니다. AI 모델 중 **선형 회귀(Linear Regression)**나 인공 신경망 같은 모델들이 Regression 문제를 해결하는 데 사용될 수 있습니다.
* Regression의 뜻? *
회귀(Regression)라는 용어는 통계학에서 유래했으며, 그 이름이 붙은 이유는 역사적으로 "평균으로의 회귀"(regression toward the mean) 현상에서 비롯되었습니다. 이 개념은 19세기 통계학자인 프랜시스 골턴(Francis Galton)이 연구한 내용에서 등장했는데, 그는 부모의 키와 자녀의 키를 비교하는 실험에서 부모의 키가 매우 크거나 작더라도 자녀의 키는 평균에 가까운 값으로 회귀하는 경향을 발견했습니다. 이 현상을 설명하기 위해 "회귀"라는 용어를 사용한 것입니다.
회귀 분석(Regression Analysis)은 입력 변수와 출력 변수 사이의 관계를 모델링하는 방법인데, 여기서 "회귀"는 원래 의미와는 다르게 값이 어디로 다시 돌아간다는 의미보다는, 입력 변수로부터 예측을 통해 출력 값을 추정한다는 의미로 해석됩니다.
즉, 회귀라는 용어는 역사적으로 "평균으로 되돌아가는 경향"을 나타냈지만, 현재 회귀 분석에서는 주어진 데이터를 기반으로 연속적인 값을 예측하는 모델을 의미합니다. "돌아간다"는 의미는 현대의 회귀 문제와는 직접적으로 관련이 없습니다.
1.2. Linear Regression (선형 회귀)
Linear Regression는 입력 x와 출력 y 사이의 선형 관계를 설명하는 모델이다. 모델의 목표는 입력과 출력 사이의 관계를 선형 관계로 설명하는 것이다.
이 관계를 실제 함수로 나타낸 것이 Hypothesis Function(가설 함수)이다.
1.3. 왜 Linear(선형)로 문제를 가정하는 것일까?
현실에서 많은 데이터는 비선형적인 관계를 보인다. 입력과 출력이 일정한 비율로 변하지 않는 경우가 많다는 뜻이다.
선형 회귀는 간단한 모델로, 데이터를 분석할 때 처음에는 선형 관계를 가정하여 단순하고 해석이 쉬운 모델로 만들어 현실을 해석하기 위함이다.
1.4. Hypothesis Function(가설 함수)
Hypothesis Function(가설 함수)는 선형 회귀 모델을 표현하는 함수이다. Linear Regression 모델의 Hypothesis Function은 모델이 학습한 관계를 사용하여 예측 값을 계산하는 데 사용된다.
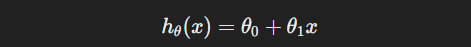
이 가설 함수는 입력 데이터 x에 대해 예측 값 h(x)를 계산한다. 모델이 학습될수록 파라미터 와 θ1은 모델을 대표하는 값에 가까워진다.
즉, 가설 함수는 선형 회귀 모델의 구현체라고 할 수 있다.
2. Hypothesis Function을 최적화하는 방법인 Loss Function!
Loss function(손실 함수)는 모델이 예측한 값과 실제 값 간의 차이를 측정하여 그 차이를 최소화하는 방향으로 Hypothesis Function의 파라미터(가중치와 절편)을 조정한다.
- Loss Function
언급한 바와 같이 손실 함수(loss function)는 모델이 예측한 값과 실제 값 간의 차이를 측정하는 함수이다. Linear Regression에서는 일반적으로 Mean Squared Error(MSE, 평균 제곱 오차)를 사용한다.
MSE 손실 함수는 다음과 같다.
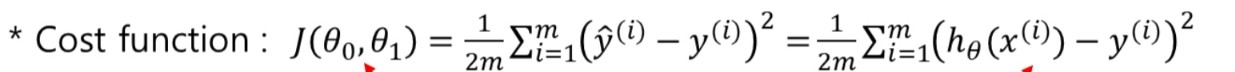
- y: ground truth(예측된 값)
- 1/2: 미분을 했을 때 편한 계산을 위한 가중치
- 절댓값으로 하지 않고 차의 제곱을 하는 이유: 미분 가능하기 때문
- m: training samples의 개수
'학부 수업 내용 정리 > 인공지능심화' 카테고리의 다른 글
| #8 Decision Tree (1) (0) | 2024.10.01 |
|---|---|
| #7 Introduction to Optimization (0) | 2024.10.01 |
| #4 Regression(3) (0) | 2024.10.01 |
| #3 Regression(2) (0) | 2024.10.01 |
| #1 AI 목적과 학습과정: 인간 인지의 모방과 추상화 (0) | 2024.09.05 |