Non-linear data structure
Data structure의 유형은 linear 구조와 non-linear 구조로 나뉜다. 두 구조의 차이는 데이터 간의 연결 방식과 접근 방식에 있다.
- linear 구조: 데이터가 일렬로 나열되어 있으며, 앞에서부터 차례대로 inedx를 통해 순서대로 접근한다. (배열, 스택, 큐)
- non-linear 구조: 구조가 나무처럼 가지가 뻗어나가거나, 도로처럼 서로 연결된 구조이다. 순차적인 접근이 아닌 연결 관계를 따라 탐색한다. (트리, 그래프)
접근 방식이 복잡하더라도 non-linear 구조를 사용하는 이유는 현실 세계의 데이터와 관계가 비선형적이기 때문이다. 예를 들어, 도시와 도시 간의 도로망, 사람들 간의 친구 관계처럼 계층적인 관계를 표현할 때 non-linear 구조가 필요하다.
Basic concept of tree
Definition
Tree는 non-linear 자료구조로 각 node 하나의 parent를 가지고, 0개 이상의 자식을 가질 수 있다.
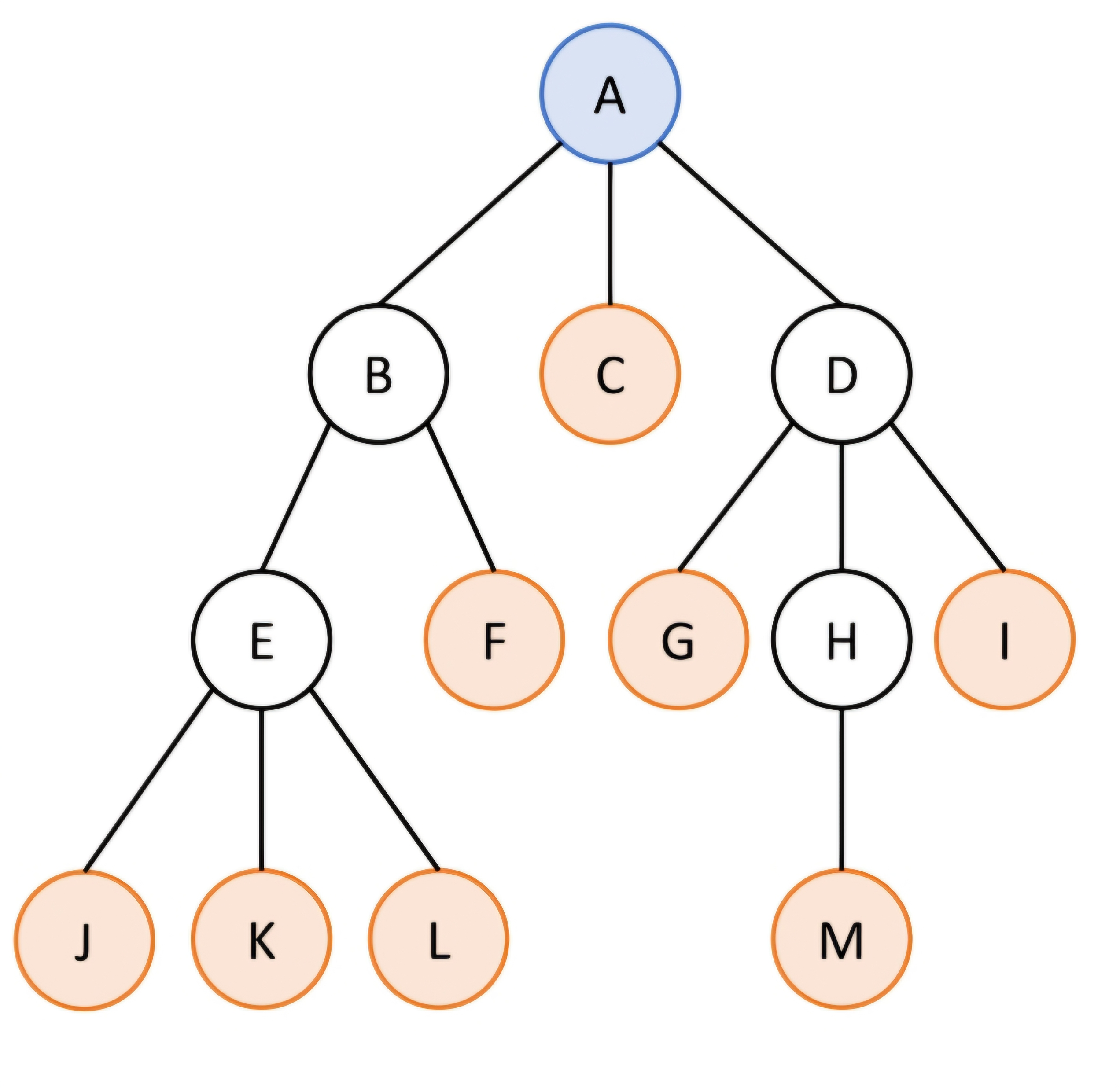
components
- Node: 데이터를 담고 있는 동그라미 형태의 기본 단위
- Edge: Node와 node를 연결하는 선
- Root: tree의 가장 위에 있는 node
- Terminal (leaf) node: tree의 가장 하단의 node
- non-Terminal node: root도 아니고 leaf도 아닌 node
Parent, child & sibling nodes
- Parent (부모 노드): Node를 상위에서 연결한 node
- E: B
- H: D
- M: H - Child (자식 노드): Node 하위에 연결된 node
- B: E, F
- E: J, K, L
- C - Sibling (형제 노드): 한 부모에서 나온 옆에 있는 node
- J: K, L
- I: G, H
Ancestor & descendant nodes
- Ancestor (조상 노드, 엔쎄스털): N의 Ancestor는 N에서 root에 이르는 경로에 있는 모든 상위 Node들
- J: E, B, A
- C: A
- G: D, A - Descendant (후손 노드, 디쎈던트): 어떤 node N에서 leaf에 이르는 경로에 있는 모든 하위 Node들
- E: J, K, L
- D: G, H, I, M
Degree & level
- Degree (차수): 정점에 연결된 간선의 개수, 자식의 수
- A: 3
- B: 2
- H: 1 - Level (레벨): 현재 node가 root로부터 얼마나 떨어져 있는지를 나타내는 수치
- A: 1
- K: 4
- G: 3
Height
Height는 어떤 노드에서 leaf까지의 거리이다.
- A: 3
- J: 0
- G: 0
- H: 1
Subtree
Tree는 항상 복수 개의 sybtree로 나뉠 수 있다.
Binary Tree(이진 트리)
Binary Tree?
각 node의 최대 차수가(degree) 2이거나 자식을 가지지 않는 tree 구조이다.
Height 범위
Node의 개수가 N일 때 tree의 구조에 따라 height이 달라질 수 있다.
Minimum height
Node가 좌우게 고르게 분포된 tree일 경우 height는 log₂(N) 꼴이 되며 height는 정수이므로 소수는 내림하여 정수로 표현한다.
height = ⌊log₂N⌋
Maximum heigth
모든 node가 한 쪽으로만 이어진 편향된 구조일 경우 tree는 linear 구조이며 height는 N-1이다.
Subtype of Binary trees
- Full Binary Tree (포화 이진 트리): 모든 node가 0개 또는 2개의 children node를 가지는 tree, 모든 node의 children의 개수가 0 혹은 2인지를 통해 판단한다.
- Perfect Binary Tree (완전 포화 이진 트리): Full binary tree의 일종으로 모든 leaf node가 동일한 level에 있는 tree, 모든 level이 가득 차있는지로 판단한다.
- Complete Binary Tree (완전 이진 트리): leaf level을 제외한 모든 level은 꽉 차 있고, 마지막 level은 왼쪽부터 순서대로 채워진 tree, 약간 덜 채워졌지만 왼쪽 정렬된 느낌이다.
- Balanced Binary Tree (균형 이진 트리): 모든 노드의 왼쪽, 오른쪽 subtree의 height 차이가 1 이하인 tree, 물론 한 쪽만 무거워 보여도 왼쪽과 오른 쪽 subtree의 height 차이가 1 이하면 된다.
- Skewed tree(편향 이진 트리, 스큐드): 모든 node가 한 쪽 자식만 가지는 tree
'학부 수업 내용 정리 > 자료구조' 카테고리의 다른 글
| Queue (0) | 2025.04.04 |
|---|---|
| Stack (0) | 2025.03.31 |
| Variation of linked lists (0) | 2025.03.23 |
| Complexity (0) | 2025.03.22 |
| Linked lists (0) | 2025.03.18 |